A_MATEMATİM
MATEMATİK FORMÜLLERİ
ÜSLÜ SAYILAR
x . an + y . an – z . an = (x + y – z) . an
am . an = am + n
am . bm = (a . b)m
am : an = am - n
KARE'NİN ALANI:
A=a.a
(a karenin bir kenarı)
DİKDÖRTGEN'İN ALANI:
A = a.b
(a kısa kenarı, b uzun kenarı)
YAMUK'UN ALANI:
A = (a+c).h / 2
(a alt taban uzunluğu, c üst taban uzunluğu, h yükseklik)
PARALELKENAR'IN ALANI:
A = a.h
(a taban kenarı, h tabana inen yükseklik)
SİLİNDİR'İN HACMİ:
H = taban alan.yükseklik
H = π.r.r.h
(π=3,14 alırız, r taban yarıçapı, h yükseklik)
(konserve tenekesi)
KÜP'ÜN HACMİ:
H = a.a.a
(a küpün bir kenarının uzunluğu)
(küp şeker)
DİKDÖRTGENLER PRİZMASI'NIN HACMİ:
H = a.b.c
(a en, b boy, c yüksekliği)
(kibrit kutusu)
KARE PRİZMA'NIN HACMİ:
H = taban alan.yüksekliği H = a.a.b
(a kare olan tabanın bir kenarı, b yükseklik)
DİK PRİZMALARIN HACMİ:
V= (taban alanı) X (yükseklik)
ÇEMBER'İN VE DAİRE'NİN ÇEVRESİ:
Ç = 2.π.r
(π=3,14 alırız r daire veya çemberin yarıçapı)
DAİRE'NİN ALANI:
A = π.r.r
(π=3,14 alırız r dairenin yarıçapı)
DAİRE DİLİMİNİN ALANI:
A = π.r.r.x / 360º
(π=3,14 alırız r dairenin yarıçapı, x açısı daire diliminin arasında kalan merkez açı)
ÇEMBER YAYININ UZUNLUĞU:
Ç = 2.π.r.x / 360º
(π=3,14 alırız r çemberin yarıçapı, x açısı çember parçasının arasında kalan merkez açı)
ÜÇGENİN ALANI VE ÇEVRESİ
Üçgenin çevresini bulabilmek için
kenarlar toplanır.
Ç = a + b + c
Üçgenin alanını bulmak için yükseklikle
kenar çarpılır ve ikiye bölünür.

h x a
A= ----------
2
ÇOKGENDE iç açılar toplamı: Dış bükey bir çokgenin n tane kenarı var ise iç açılarının toplamı
(n - 2) . 180°
Dış açılar toplamı: Bütün dışbükey çokgenlerde
Dış açılar toplamı =360°
Köşegenlerin sayısı: n kenarlı dışbükey bir çokgenin
n.(n-3) / 2
Bir köşeden (n – 3) tane köşegen çizilebilir.
n kenarlı dışbükey bir çokgenin içerisinde, bir köşeden köşegenler çizilerek
(n – 2) adet üçgen elde edilebilir.
n kenarlı düzgün bir çokgende bir iç açının ölçüsü
(n - 2) . 180°/ n
Konveks çokgenlerin dış açıları toplamı 360° olduğundan düzgün çokgenin bir dış açısının ölçüsü
360° / n
DOĞRUNUN EĞİMİ
Eğim karşının komşuya bölümüdür.
Eğim=tanx

Eğim=b/c
Kar-Zarar Problemleri
Maliyet:100 %20 kar Satış:100+20=120
Maliyet:100 %20 İndirimli Satış:
100-20=80
İndirimli satışın üzerinden %20 karlı satış:
80.%120=(80.120):100=96
YÜZDE PROBLEMLERİ
Yüzde, paydası 100 olan kesirlere denir.
|
Örneğin, yüzde 50 (%50)= 50/100 = 1/2
|
|
|
Yüzde 20 (%20) = 20/100 = 1/5
|
FAİZ PROBLEMLERİ
f = a.n.t / 100 (yıllık faiz)
f = a.n.t / 1200 (aylık faiz)
f = a.n.t / 36000 (günlük faiz)
(a anapara, n faiz yüzdesi, t zaman, f faiz)
SAAT PROBLEMLERİ
|30.saat(akrep)-5,5.dakika(yelkovan|
=kollar arasındaki açı
HAREKET PROBLEMLERİ
Yol: x
Hız: v
Zaman: t
Yol= Hız . Zaman x=v.t
Hız = Yol / Zaman v=x/t
Zaman= Yol / Hız t=x/v
Hareketliler aynı anda ve zıt yönde ise x = (v1 + v2). t
Hareketliler aynı anda ve aynı yönde
ise x = (v1 - v2). t
Nehir problemlerinde ise her zaman kayığın hızından akıntının hızı çıkartılır.
YAŞ PROBLEMLERİ
Bir kişinin yaşı a olsun,
T yıl önceki yaşı : x-T
T yıl sonraki yaşı : x + T olur.
İki kişinin yaşları oranı yıllara
göre orantılı değildir.
n kişinin yaşları toplamı b ise
T yıl sonra b + n.T
T yıl önce b - n.T
Kişiler arasındaki yaş farkı
her zaman aynıdır.
x yıl öncede yaş farkı a-b
x yıl sonrada yaş farkı a-b
Katlar ve oranlar hangi yılda verildiyse
denklem o yılda kurulur.
İŞÇİ - HAVUZ PROBLEMLERİ
Bir işi;
A işçisi tek başına a saatte,
B işçisi tek başına b saatte,
C işçisi tek başına c saatte
yapabiliyorsa;
İş t saatte bitiyorsa
1/a + 1/b + 1/c = 1/t olur.
A işçisi 1 saatte işin 1/a sını bitirir.
A ile B birlikte t saatte işin
(1/a + 1/b).t sini bitirir.
A işçisi x saatte, B işçisi y saatte
C işçisi z saatte
çalışarak işin tamamını bitirdiklerine göre üçü birlikte işi k saatte bitiriyorsa,
k/x + k/y + k/z = 1 olur.
Havuz problemleri işçi problemleri
gibi çözülür.
A musluğu havuzun tamamını a saatte
doldurabiliyor.
Tabanda bulunan B musluğu dolu havuzun
tamamını tek başına b saatte boşaltabiliyor
olsun.
Bu iki musluk birlikte bu havuzun t saatte
(1/a - 1/b).t sini doldurur.
Bu havuzun dolması için b > a olmalıdır.
Eğer havuz t saatte doluyorsa
1/a - 1/b = 1/t
Havuz dolduruluyorsa dolduran musluk (+), boşaltan musluk (-) alınır.
Havuz boşaltılıyorsa dolduran musluk (-), boşaltan musluk (+) alınır.
TRİGONOMETRİ

SinC = karşı / hipotenüs
SinC = c / a
CosC = komşu / hipotenüs
CosC = b / a
TanC = karşı / komşu
TanC = c / b
CotC = komşu / karşı
CotC = b / c
tanx = sinx / cosx
cotx = cosx / sinx
tanx . cotx = 1
sinx.sinx + cosx.cosx = 1
ÖZDEŞLİKLER
İki Kare Farkı - Toplamı
I) a2 – b2 = (a – b) (a + b)
II) a2 + b2 = (a + b)2 – 2ab ya da
a2 + b2 = (a – b)2 + 2ab dir.
İki Küp Farkı - Toplamı
I) a3 – b3 = (a – b) (a2 + ab + b2 )
II) a3 + b3 = (a + b) (a2 – ab + b2 )
III) a3 – b3 = (a – b)3 + 3ab (a – b)
IV) a3 + b3 = (a + b)3 – 3ab (a + b)
Tam Kare İfadeler
I) (a + b)2 = a2 + 2ab + b2
(a + b)2 = (a – b)2 + 4ab
II) (a – b)2 = a2 – 2ab + b2
(a – b)2 = (a + b)2 – 4ab
III) (a + b + c)2 = a2 + b2 + c2 + 2(ab + ac + bc)
IV) (a + b – c)2 = a2 + b2 + c2 + 2(ab – ac – bc)
(a + b)3 = a3 + 3a2b + 3ab2 + b3
(a – b)3 = a3 – 3a2b + 3ab2 – b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 +b4
(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
PİSAGOR BAĞINTISI

a2=b2+c2
a.a=b.b+c.c
OLASILIK
P(A)=S(A) / S(E)
Bir olayın olasılığı=istenilen durumların sayısı / tüm durumların sayısı
p(A)=0 ise imkansız olay=gerçekleşmesi mümkün değil
P(A)=1 ise kesin olay=gerçekleşmesi kesin
Herhangi bir olayın olmama olasılığı:
P'(A) = 1 - P(A)
Bağımsız olay:
Birbirlerini etkilemiyorlarsa(para-zar)
P(A Ç B)= P(A) . P(B)
Ayrık iki olayın birleşiminin olasılığı:
P(AUB)= P(A) + P(B)
Ayrık olmayan iki olayın birleşiminin olasılığı:
P(AUB)= P(A) + P(B) - P(A ÇB)
n elemanlı bir kümenin r elemanlı permütasyonu:
P(n,r)=n! / (n-r)!
P(n,n)= n! p(0,0)= 1
P(n,0)= 1 P(n,1)= n
Dairesel Permütasyon: (n-2)!
KOMBİNASYON
n elemanlı kümenin r ' li kombinasyonları sayısının formülü,
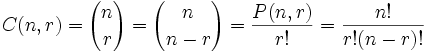
FAKTÖRİYEL
n!=1.2.3.4.5.........n
6!=1.2.3.4.5.6=720
ORANTI
1) a/b=c/d ise a.d= b.c
2) a : b : c = x : y : z ise,
Burada, a = x . k
b = y . k
c = z . k dır.
B-GEOMETRİ
GEOMETRİ FORMÜLLERİ
Üçgenler,üçgende açı kenar ilişkileri,üçgen çeşitleri,üçgende alan,çember ve daire,benzerlik teoremleri,çokgenler,dörtgenler ve daha birçok geometri formülleri yer almaktadır.




www.matematikcifatih.tr.gg












www.matematikcifatih.tr.gg

FİZİK FORMÜLLERİ
ELEKTRİK - MANYETİZMA
| Elektrik alanındaki parçacığın ivmesi |
 |
| Ampere yasası |
 |
| Biot-Savart yasası |
 |
| Silindirik yüzeylerin sığası (kapasitansı) |
 |
| Paralel yüzeylerin sığası (kapasitansı) |
 |
| Nokta yükte elektrostatik potansiyel enerji değişikliği |
 |
| Potansiyel değişikliği |
 |
| İletken bantta akım |
 |
| Elektrik akımı |
 |
| Elektromanyetik dalgalarda elektrik alanı/manyetik alan ilişkisi |
 |
| Halka yükün eksenindeki elektrik alanı |
 |
| Elektriksel akı tanımı |
 |
| EMF (elektromotiv kuvvet) tanımı |
 |
| Gauss yasası |
 |
| Akım halkasının manyetik dipol momenti |
 |
| Bobin içindeki manyetik alan |
 |
| Manyetik akı tanımı |
 |
| Hareket eden yükteki manyetik kuvvet |
 |
| Maxwell denklemi, Faraday yasası |
 |
| Maxwell denklemi, Gauss yasası |
 |
| Yük taşıyıcıların sayı yoğunluğu |
 |
| Ohm yasası |
 |
| Çizgisel şarj potansiyeli |
 |
| Poynting vektörü |
 |
| Direnç, rezistans |
 |
| Bobinin self-indüktansı |
 |
| Akım halkasının torku |
 |
| Voltaj denklemi |
 |
| Manyetik alan için dalga denklemi |
 |
| Yukawa potansiyeli |
 |
MEKANİK
| Açısal momentum |
 |
| Ortalama ivme |
 |
| Hacim modülüsü tanımı |
 |
| Merkezcil ivme |
 |
| Kompresibilite |
 |
| Süreklilik denklemi |
 |
| Yer değiştirme |
 |
| Hidrolik kaldırma kuvveti |
 |
| Anlık ivme |
 |
| Newton yasası II |
 |
| Makaslama modülüsü tanımı |
 |
| Makaslama gerilimi (stresi) |
 |
| Basit harmonik hareketin ivmesi |
 |
| Ses dalgalarının sıvıdaki hızı |
 |
| Yay sabiti |
 |
| Gerilim, stres |
 |
| Hız |
 |
| Hız |
 |
| Visköz akış |
 |
| Young modülüsü |
 |
MODERN FİZİK
| Kara-delik entropisi (Hawking) |
 |
| Kara-delik sıcaklığı |
 |
| de Broglie dalga boyu |
 |
| Relativistik kütle-enerji ilişkisi (Einstein) |
 |
| Rydberg sabiti |
 |
| Kara-delik çapı (Schwarzschild) |
 |
| Zamana bağımlı Schrödinger denklemi (1D) |
 |
| Zamandan bağımsız Schrödinger denklemi (1D) |
 |
OPTİK
| Tek yarıklı kırınımda birinci ve sonuncu dalga arasındaki faz farkı |
 |
| Kırılma indeksi |
 |
| Tek yarıklı kırınımda sıfır noktaları yoğunluğu |
 |
DALGA
| Süregiden salınımın genliği |
 |
| Sönümlenen salınımın açısal frekansı |
 |
| Vuru frekansı |
 |
| Süregiden salınımda yer değiştirme |
 |
| Yavaş sönümlenen salınımda yer değiştirme |
 |
| Sönümlenen salınımdaki enerji değişimi |
 |
| Sönümlenen salınımdaki enerji değişimi |
 |
| Harmonik dalga tarafından iletilen enerji |
 |
| Harmonik dalga fonksiyonu |
 |
| Harmonik dalga fonksiyonu |
 |
| Basit harmonik hareketin kinetik enerjisi |
 |
| Süregiden salınımın faz sabiti |
 |
| Basit harmonik hareketin potansiyel enerjisi |
 |
| Harmonik dalga tarafından iletilen güç |
 |
| Duran-dalga (durağan-dalga) fonksiyonu |
 |
| Duran-dalgaların her iki ucu sabit olan bir ip üzerindeki süperpozisyonu |
 |
| Basit harmonik hareketin toplam enerjisi |
 |
| Süregiden salınımın rezonans frekansındaki hızı |
 |
TERMODİNAMİK
| Bir nesneden ışınan net güç |
 |
| Bir nesnece soğurulan ışıma |
 |
| Stefan-Boltzmann yasası |
 |
| Isıl iletim |
 |
| Isıl direnç |
 |
Yayda Depolanan EnerJİ

U: yayda depolanan enerji
k: sabit
x: uzanım
Yayda Geri Çağırıcı Kuvvet

F: geri çağırıcı kuvvet
k: sabit
x: uzama
Periyot

T: periyot (s)
f: frekans (1/s)
Periyot (basit sarkaç)

T: sarkacın periyodu (s)
l: sarkacın uzunluğu (m)
g: yerçekimi ivmesi (m/s^2)
Potansiyel Enerji

U: potansiyel enerji (joule)
m: kütle (kg)
g: yerçekimi ivmesi (m/s^2)
h: yükseklik (m)
Periyot (yayda)

Ts: Yaya bağlı salınım yapan cismin periyodu
m: kütle
k: sabit
İş

W: iş (joule)
F: cisme etkiyen kuvvet (Newton)
Δ
x: alınan yol (metre)
θ: Kuvvet vektörü ile hareket doğrultusu arasındaki açı
Kinetik Enerji

K: kinetik enerji (kg.m^2/s^2)
m: kütle (kg)
v: hız (m/s)
Güç

P: Güç
F: Kuvvet
v: Hız
θ: Kuvvet ve hız vektörü arasındaki açı
Kütle Çekim Kuvveti
 M1,2:
M1,2: cisimlerin kütleleri
R: aralarındaki uzaklık
G: 6,6710 − 11
Nm2
kg − 2 değerinde olan evrensel kütleçekim sabiti
Düzgün Hızlanan Doğrusal Harekette Konum

V0: İlk hız (m/s)
a: ivme (m/s^2)
x0: ilk konum (m)
t: zaman (s)
x: son konum (m)
Merkezcil İvme

ac = merkezcil ivme (m/s^2)
v = açısal hız (m/s)
r = dairesel harekette yarıçap
Tork

τ =
Tork (N.m)
r: Kuvvet kolu (m)
F: Kuvvet (N)
θ= açı
Düzgün Hızlanan Doğrusal Harekette Hız (Zamansız)
Hız ve ivme vektörel niceliklerdir.

V: Hız (m/s)
V0: İlk hız (m/s)
a: ivme (m/s^2)
x0: ilk konum
x: son konum
Düzgün Hızlanan Doğrusal Harekette Hız
Hız ve ivme vektörel niceliklerdir.
V = V0 + a.t
V: Hız (m/s)
V0: İlk hız (m/s)
a: ivme (m/s^2)
t: geçen zaman (s)
Momentum
Bir cismin momentumu cismin hızı ile kütlesinin çarpımına eşittir.
P=m.V
P: momentum (kg.m/s)
m: kütle (kg)
V: hız (m/s)
İtme (Impuls)
İtme bir cismin momentumunda meydana gelen değişikliğe eşittir.
I= F.Δt = ΔP
I= İtme
F = Kuvvet
Δt = Kuvvetin etkili olduğu zaman aralığı
ΔP = Δt zaman aralığında momentumda meydana gelen değişim
Newton'un 3. Kanunu
Bir cisme etki eden kuvvet bu kuvvete eşit ama zıt yönde başka bir kuvvetin doğmasına neden olur. Bu kuvvete tepki kuvveti denir.
Fetki=Ftepki
Newton'un İkinci Kanunu
Bir cisim üzerine etkiyen kuvveti cisme kuvvet ile aynı yönde bir ivme kazandırır. Bu ivme cimin kütlesi ile doğru orantılıdır.
F=m.a
F: kuvvet (N)
m: kütle (kg)
a: ivme(m/s^2)
KİMYA

İlk 20 Element İsimleri ve Sembolleri:
| 1 |
Hidrojen |
H |
|
11 |
Sodyum |
Na |
| 2 |
Helyum |
He |
12 |
Magnezyum |
Mg |
| 3 |
Lityum |
Li |
13 |
Alüminyum |
Al |
| 4 |
Berilyum |
Be |
14 |
Silisyum |
Si |
| 5 |
Bor |
B |
15 |
Fosfor |
P |
| 6 |
Karbon |
C |
16 |
Kükürt |
S |
| 7 |
Azot |
N |
17 |
Klor |
Cl |
| 8 |
Oksijen |
O |
18 |
Argon |
Ar |
| 9 |
Flor |
F |
19 |
Potasyum |
K |
| 10 |
Neon |
Ne |
20 |
Kalsiyum |
Ca
|
| Element |
Vücudumuzda |
Yeryüzünde |
| Oksijen |
% 65 |
% 46,6 |
| Karbon |
% 18 |
|
| Hidrojen |
% 10 |
|
| Azot |
% 3 |
|
| Kalsiyum |
% 2 |
% 3,6 |
| Fosfor |
% 1,1 |
|
| Potasyum |
% 0,35 |
% 2,6 |
| Sülfür |
% 0,25 |
|
| Sodyum |
% 0,15 |
% 2,8 |
| Magnezyum |
% 0,05 |
% 2,1 |
| Demir |
% 0,004 |
% 5 |
| Silisyum |
———– |
% 27,7 |
| Alüminyum |
———– |
% 8,1
|
BİLEŞİK FORMÜLLERİNİN BULUNMASI
Bileşik formülleri basit formül ve molekül formülü olmak üzere iki türlüdür:
-
Basit (Ampirik) Formül
-
Basit formül, bir bileşikteki elementlerin türünü ve atom sayılarının oranını gösterir.
-
CH2, CH2O, NO2 .....gibi
-
Basit formül bulmak için:
Bir bileşikteki elementlerin kütlece yüzde bileşimi (ya da sabit kütle oranı) ile elementlerin atom kütlelerini (ya da atom kütleleri arasındaki oranı) bilmek yeterlidir.
Örn; X ve Y’den oluşan bir bileşikte sabit kütle oranı 7 ise, bileşiğin basit
3
formülü nedir? (X=14, Y=12)
Atom sayılarını bulmak için verilen element kütleleri atom kütlelerine bölünür.
nx = 7 = 0,5 ny = 3 = 0,25
-
12
değerleri yerlerine yazıldığında X0,5 Y0,25 bulunur.Bu bileşikte katsayılar 0,25’e bölünerek kısaltılır ve basit formül X2Y bulunur.
-
Molekül Formülü
C2H6O2, C6H12O6.... gibi.
-
Yanma Tepkimelerinde:
nicelikleri bilinmelidir.Böylece tepkime eşitlenerek 1 mol bileşikteki elementlerin atom sayıları bulunur.
-
Kütlece Bileşim Verilen Örneklerde:
-
Elementlerin kütlece yüzde bileşimi (sabit kütle oranı)
-
Elementlerin atom kütleleri
-
Bileşiğin mol kütlesi (ya da örneğin özkütle gibi bileşiğin mol kütlesinin bulunmasını sağlayan veriler)
nicelikleri bilinmelidir.
Bileşiğin mol kütlesi biliniyorsa 1 mol bileşikteki elementlerin atom sayıları da bulunur.
Örn; CXHYO2 bileşiğinin 0,2 molü 1 mol O2 ile tam yanarak 0,8 mol CO2 ile 0,8 mol H2O oluşturuyor.Bu organik bileşiğin molekül formülü nedir?
Tepkime ile ilgili verilerden yararlanarak 1 mol CXHYO2 ‘nin yanma tepkimesindeki katsayılar bulunur.
0,2 mol 1 mol 0,8mol 0,8 mol
CXHYOZ + .........O2 ® .........CO2 +..........H2O
1 mol 5 mol 4 mol 4 mol
1 mol CXHYOZ için denkleşmiş haldeki yanma tepkimesi şöyledir:
1 CXHYOZ + 5O2 ® 4CO2 + 4H2O
Atom sayıları eşitlendiğinde x = 4, y = 8, oksijen sayıları eşitlendiğinde
Z + 10 = 8 + 4’den z = 2 bulunur.
Bu değerler 1 mol bileşikteki atomların katsayıları olduğundan molekül formülü C4H8O2 olur.